A greedy algorithm is an algorithm that follows the problem solving heuristic of making the locally optimal choice at each stage with the hope of finding a global optimum. In many problems, a greedy strategy does not in general produce an optimal solution, but nonetheless a greedy heuristic may yield locally optimal solutions that approximate a global optimal solution in a reasonable time.

- Greedy algorithm, Wikipedia

What does a greedy algorithm look like?
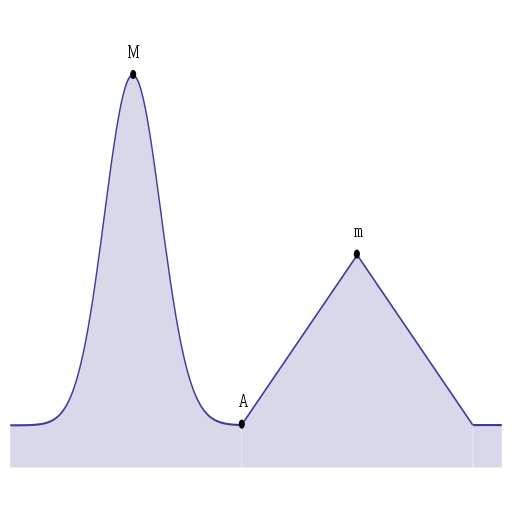
Images from Wikipedia illustrate the concept well. In the first one, we begin our search of the space for a maximum at point A. If we're greedy, the next highest point takes us along a path that maximizes at point (lower case) m. However, the optimal solution is at point (upper case) M.



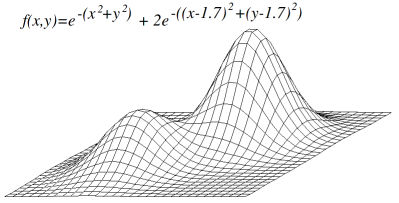
If you're greedily searching (again, for a maximum) in three-dimensional space, and start in a poor position (like near the left in the image below), you'll never make it off the shorter hill onto the taller one:



What does a greedy algorithm for yourself look like?
Perhaps we should first define what it is for which we're optimizing: To keep it simple, I'm going to identify it as maximizing income.

You could also be seeking to minimize the distance (in time) between working for clients, or minimizing the time you spend acquiring each customer -- maximization is not an intrinsic property of optimization.

I purposefully exclude things like time and happiness (or optimizing for some combination of all three). While I value those things and would like to think I've tried to optimize for them, upon closer inspection I recently realized I've tended to simply accept whatever side-effect optimizing for money has had on those values.

I think it's a fair assumption that plenty of other people are doing the same. If you're not one of them: congrats! But before you dismiss the idea entirely, you ought to consider that you might be, just to be sure.

So what does it look like? Again from Wikipedia, I like the idea of moving from node to node on a graph:



At each point in time (a vertex on the graph) we are presented with a series of options whose positive return is the value at that vertex. The options available to us are connected by the edges. (You might also assign a cost to each edge, and change your greedy-optimization heuristic to be return minus cost).

In the graphic I've used, only two options are available at each point, but in reality there are normally a lot more options from which to choose, and maybe even times when you have only one option.

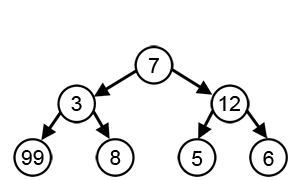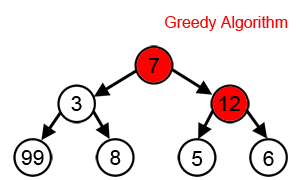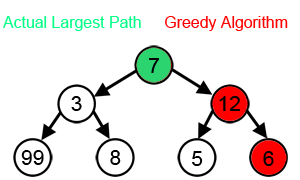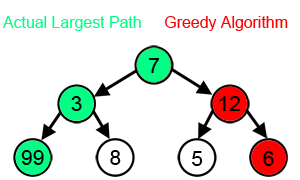
If we're starting at 7 and being greedy in our search for a maximum, we miss out on the global maximum.

You might mention -- hey, we could backtrack and search the entire space. But you might not have the resources available once you've gone down the path to 6. You might have reached your maximum workload by that point, and by the time you free up some time, the opportunity for the 99 is gone.

How do you know if you're running your business like a greedy search algorithm?
Here are some symptoms:

• Taking the first job offer or client you get when you need work
• If you're a freelancer, filling all your time with client work
• Taking the first business model that seems to be working and trying to maximize it

Can you think of any others?

Prior to last year, I was executing a totally greedy algorithm with regards to my career. But it's not just something I've noticed in myself: almost every job I've had utilized greedy methods for making money.

As part of my greedy search (which was not just about maximizing money, but more towards minimizing unemployment, even if it meant working for people who would end up stiffing me on paychecks), I ended up burning through about four months of savings (I had six). Last year though, I started making some changes to a better approach. When I made my way back up to a six month cushion and took time to reflect on some of the changes that got me there, I realized the parallels to algorithms I'd learned about in college.

Improving your odds
How can you improve your chances of finding a global (or at least higher) maximum?

In the general problem, given enough time and resources, you could do an exhaustive search -- or in our graph model, visit every node.

But I don't have the resources to exhaustively search the entire space to produce an optimal solution, and I'm betting you don't either.

Instead of straight greedy hill-climbing, we could explore some variants. My favorite here is called "shotgun hill climbing," where instead of following a path all the way to it's maximum, we'll randomly restart (but we don't forget where we came from on those restarts, in case we don't end up in a better position).

It's what I like about Amy Hoy's stacking bricks metaphor. A freelancer can start taking time between gigs (or not remain fully engaged) and spend some time developing products. Each successive product is a new brick, and over time you can build a wall.

Savings and product revenue are like ammunition for your shotgun hill climbing business algorithm. They allow you to explore different starting positions, as long as you're not being greedy with minimizing the distance (in time) between clients or booking all your time to work for others.

In practice, all those ideas you have floating around in your head (or ideas.txt file) are the different options you have in paths to take (in addition to other jobs, clients, ideas for "upselling", etcetera). You have to spend a significant piece of time on one to find out if it gets you further up the hill or not -- but not so much so that you can't get back to your last local maximum or randomly try another.

(Side note: I'm not advocating strictly random here -- you can apply some heuristic to affect the "probability" of choosing a certain idea).

Last year I took my first steps to taking a shotgun approach. This year I plan to take it further.

Thoughts? I'd love to hear them below.

Hey! Why don't you make your life easier and subscribe to the full post or short blurb RSS feed? I'm so confident you'll love my smelly pasta plate wisdom that I'm offering a no-strings-attached, lifetime money back guarantee!